|
|
|
■ 上野・竹田研の研究 ■
大気突入カプセルの数値解析

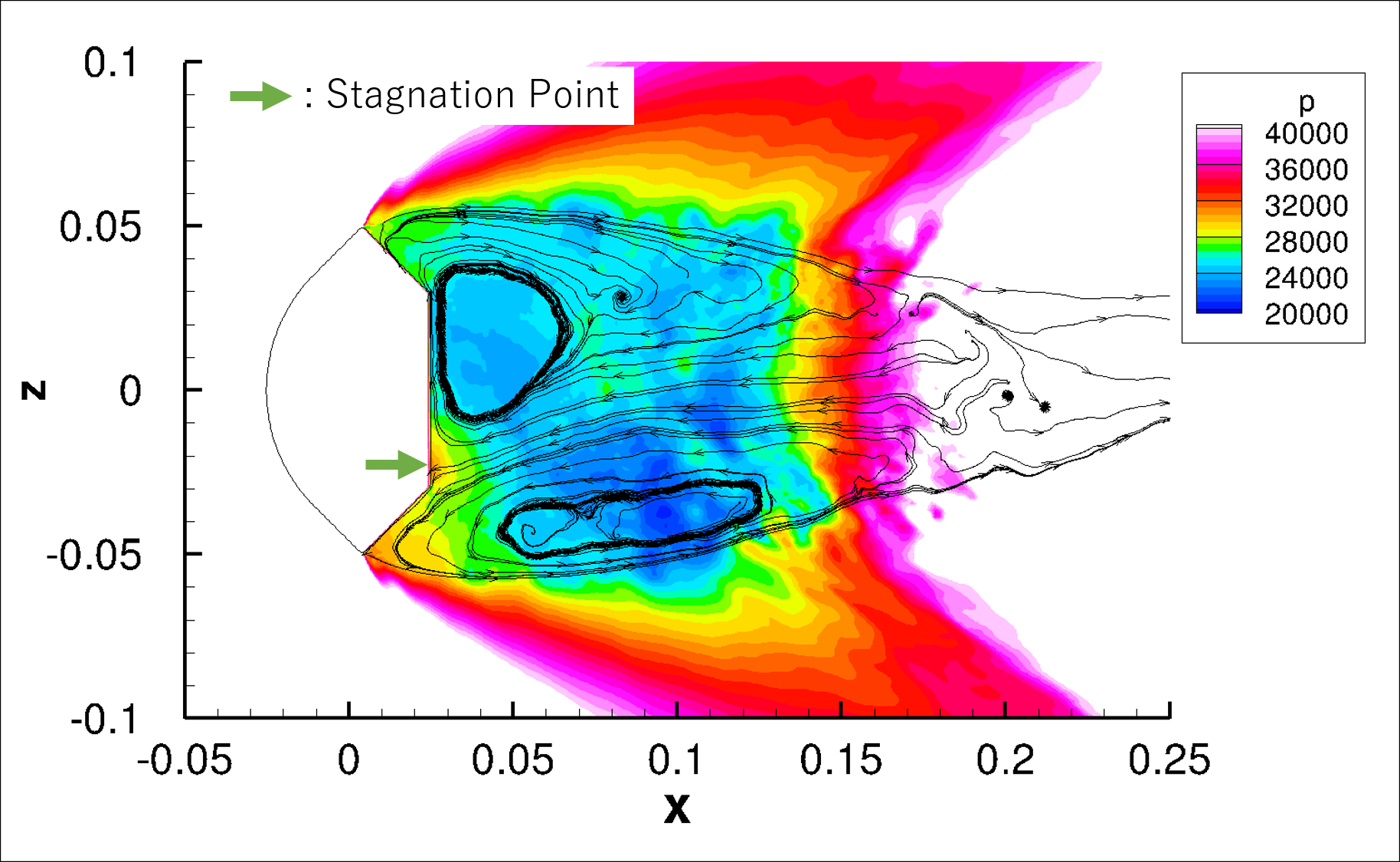
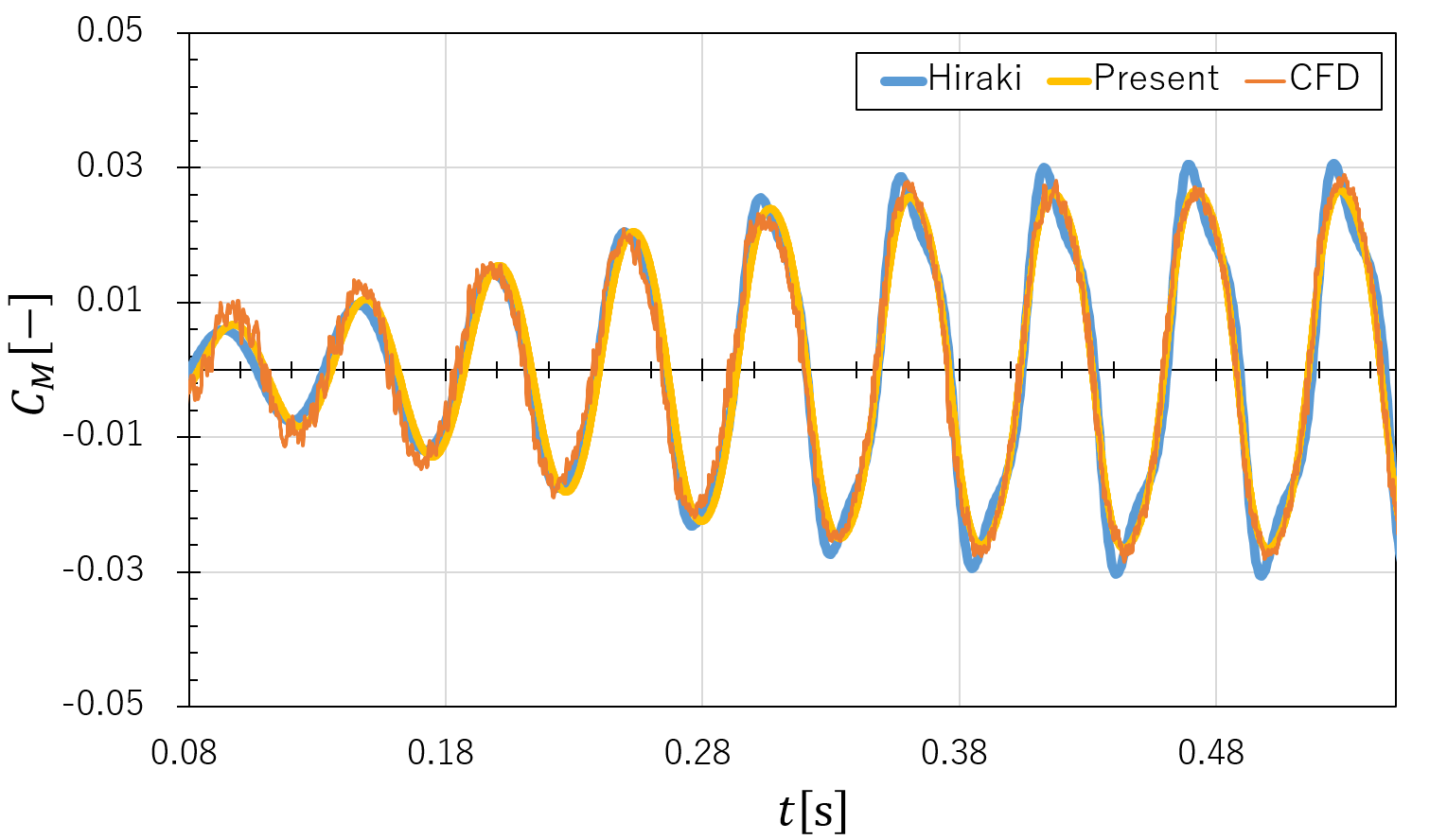
はやぶさ形状の待機突入カプセルの流体と飛行力学との連成シミュレーションを行っています。
本研究では、静止状態から流体力により振動が励起し、
振幅が一定のリミットサイクル振動に入る様子の際現に成功しました。
リミットサイクル振動時の流れ場から、振動の励起に対するピッチ角0°付近における動的に不安定なモーメントの寄与を明らかにしました.
また,新しいピッチングモーメントのモデル式を考案し,既存のモデル式を改善しました.
(Y.Takeda, K.Ueno, S.Matsuyama & H.Tanno, Trans. JSASS (2020))
壁面応力モデルを用いた高レイノルズ数流れの数値解析


乱流境界層内をモデル化した方程式から得られる
壁面せん断応力を用いた直交カットセル法の高性能化を行っています。
一般に高レイノルズ数流れにおける乱流境界層を含んだ流れを
直接シミュレーションすることは莫大な計算量となり、現実的ではありません。
私たちの研究室で開発している直交カットセル法と壁面応力モデルを組み合わせることで、
複雑形状まわりの高レイノルズ流れの高精度なシミュレーションの実現を目指しています。
(Y.Takeda, K.Ueno, T.Ishikawa & Y.Takahashi, Appl. Sci. (2020))
動的磁力支持風洞の開発
動的磁力支持風洞の開発をしています。
磁力支持装置とは、風洞模型を磁力のみで気流中に保持できる装置です。
上野・竹田研究室の装置は3自由度の自由運動試験が可能な設計になっており、
大気圏再突入カプセルの動的風洞試験を実施して空力微係数の同定と流れの可視化を行っています。
(K. Ueno, R. Nagasaka, T. Sato and M. Kikuchi, A Magnetic Suspension System for a Wind-Tunnel Model Moving by Unsteady Aerodynamic Force, Seventeenth International Conferenece on Flow Dynamics (2020).)
デンドライト成長の数値解析
私達の研究室では、デンドライト(樹枝状結晶)成長の研究をしています。
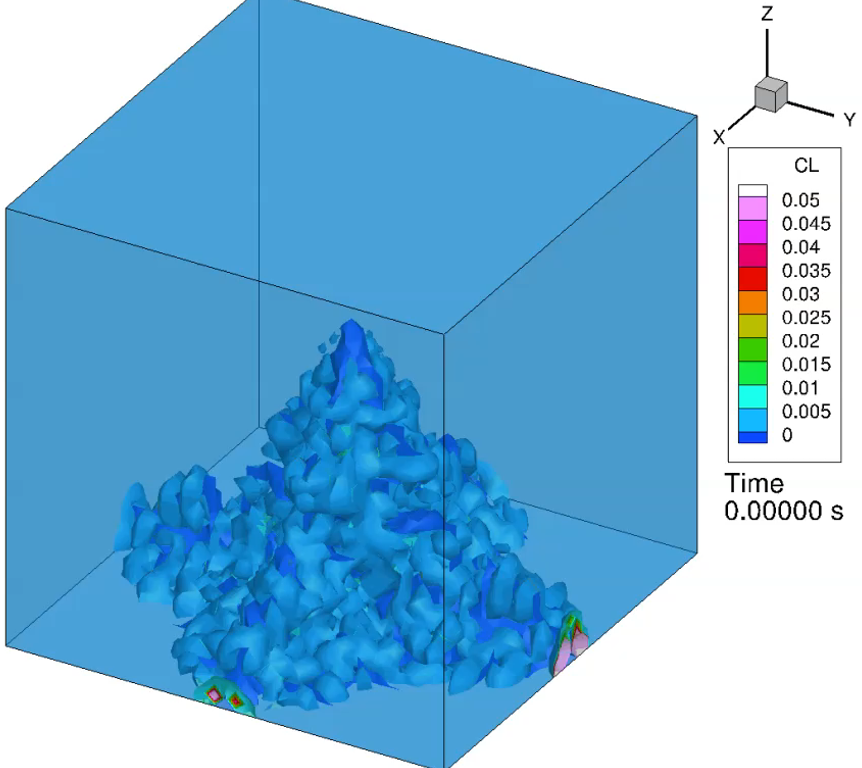
さらに、デンドライト周りの流れが結晶成長にどのような影響を与えるのか研究しています。
(上野・棗・嶋﨑・岩井・大笹,日本鉄鋼協会(2015))
流れの双極子分解と作図
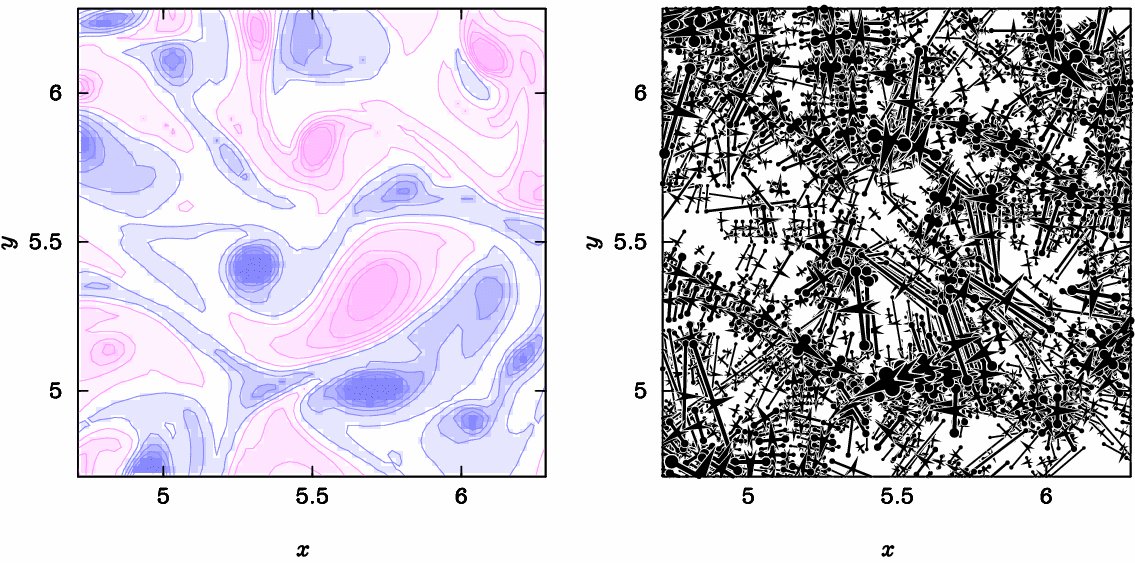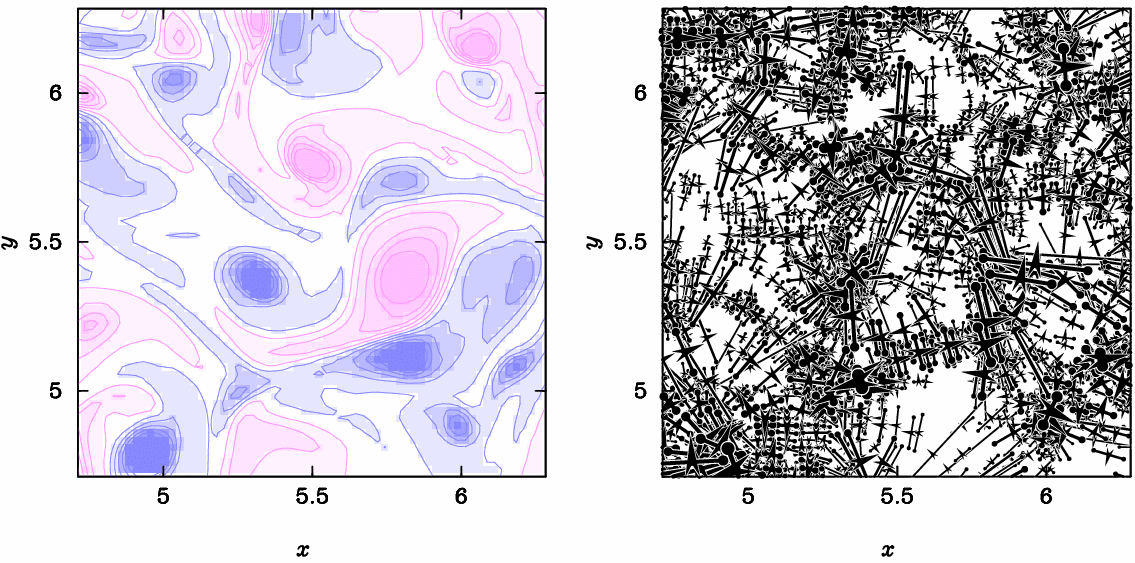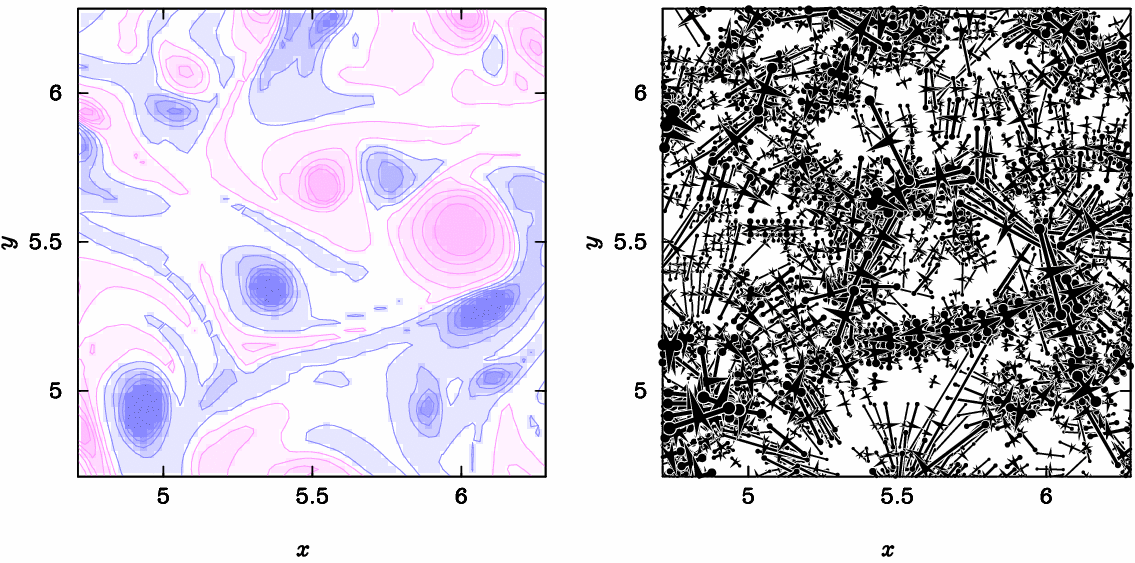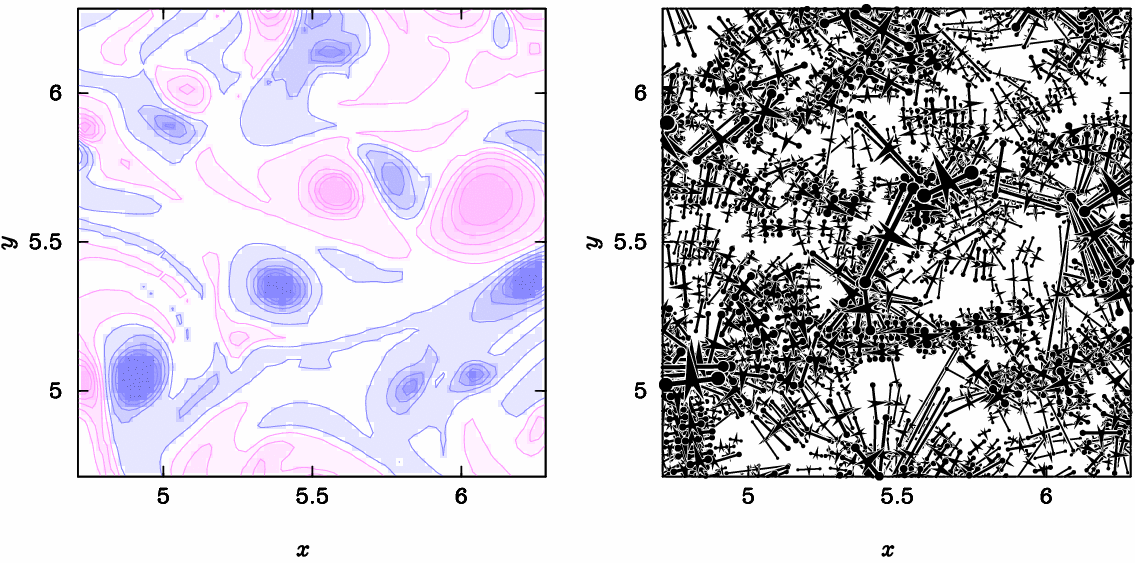
与えられた流れ場を分解して、多数の双極子流れの重ね合わせで表現する手法を研究しています。上図(左)は2次元乱流の数値解析結果(渦度を作図)です。上図(右)はこの流れを双極子に分解した結果を作図した動画です。(K.Ueno, Y.Matsumoto & K.Ishiko, J. Fluid Sci. Tech. (2017)、Y.Matsumoto, K.Ueno & T.Saito, Phys. Fluid (2009)、 Y.Matsumoto & K.Ueno, Fluid Dyn. Res. (2014))
液滴接触角の研究
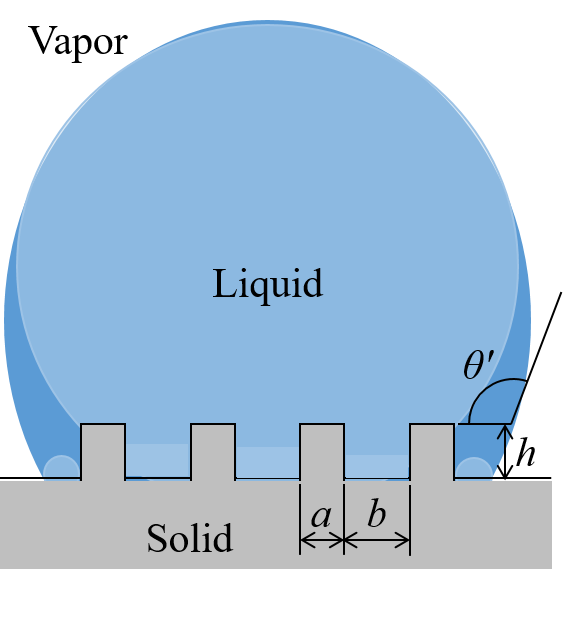

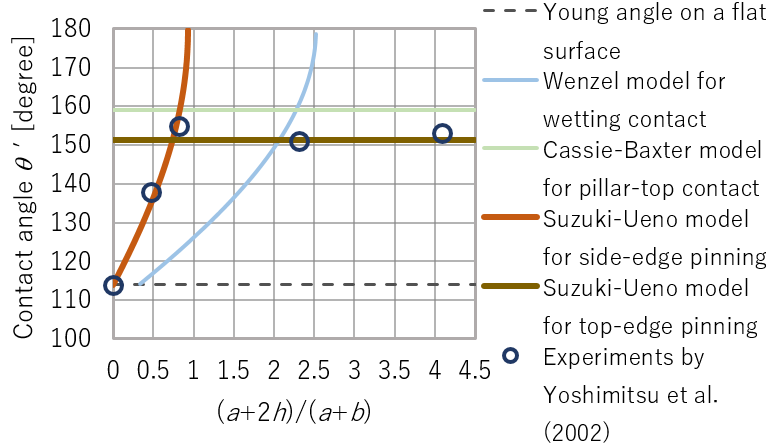
ピン止め効果を考慮してピラーパターン粗面上液滴の見かけ接触角の予測式2種 (top-edge pinning と side-edge pinning) を提案しました。ピラー高さに依存しない状況の実験データは、 Cassie-Baxter のモデルよりも Top-edge pinning モデルとよく一致しました。ピラー高さに敏感な状況の実験データは、 Wenzel のモデルでは
説明できず、 Side-edge pinning モデルで説明できました。(S.Suzuki & K.Ueno, Langmuir (2016), K.Ueno & S.Suzuki, WMS2018 (2018), )
電磁流体力学(MHD流れ)の研究
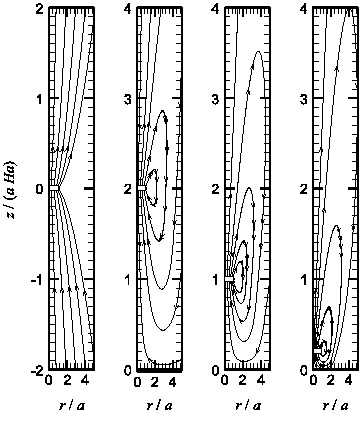
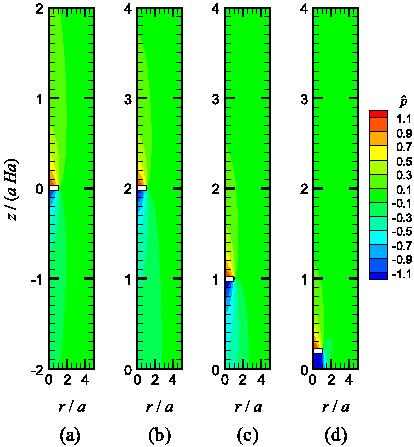
導電性流体に磁場が印加されているときの流れ(MHD流れ)の研究をしています。左図は、鉛直方向一様磁場下の導電性流体中を上昇する粒子のまわりの発生する流線を描いたものです。右図は圧力分布です。この研究では、下壁が粒子の抗力に与える影響を解明しました。(K.Ueno, S.Harada & M.Watabe, Fluid Dyn. Res. (2019)、K.Ueno & H.Yasuda, Magnetohydrodynamics (2009))
磁場下の導電性流体乱流の理論的研究
導電性流れに一様な磁場を印加(左上)した場合の、準二次元的な渦が発達(左下)と、渦の減衰率の波数依存特性(右).これまで知られていなかった、減衰の遅い三次元渦が存在することを理論的に示しました.(K.Ueno & R.Moreau, Phys. Fluid (2006))
|
|
|